統計学を学んでいて、
プログラミングをしていると、
必ず出会うのが「乱数」です。
乱数は、統計学だけでなく、機械学習や人工知能などでも避けることができない技術です。
その他、統計学を基礎とするあらゆる応用に乱数が関係してきます。
乱数のシンプルな例は、サイコロです。
プログラムの中でサイコロを振りたい場合には、乱数の知識が必要です。
サイコロを振るというのは、シンプルですが、
確率的な現象をモデル化するときの基礎でとても重要です。
例えば、現実世界をモデル化するときには、誤差の影響を考慮する必要があることがあります。
誤差は毎回決まった値が出るわけでなく、不規則な値として出てくることが多いです。
誤差を考慮してモデルを作成する場合など、
- 乱数をうまく扱う
といった技術は必須になります。
というわけで、本記事では、
- Python を使って乱数を生成させる方法
をまとめたいと思います。
特に初学者向けとして、「一様乱数」という乱数についてまとめたいと思います。
【Python 乱数】乱数とは?一様乱数とは?Python で「一様乱数」を生成させたいあなたはこちらをどうぞ【乱数とは 一様乱数とは】
乱数とは?
「乱数」というのは、
- 数字が不規則に現れる数の配列
のことです。
数字は不規則に生成されるので、次に出る数は予測できないことになります。
一様乱数とは?
「一様乱数」の「一様」というのは、
- 出てくる数値は全部同じ確率
という意味です。
なので、一様乱数はで
- 数値は不規則に出てくる
- それぞれの数値が出てくる確率は同じ
ものになります。
一様乱数の具体例は?
具体的には、1−6の範囲の整数を、一様乱数として発生させるとすると、
1、2、3、4、5、6
の数字が不規則に、同じ確率で出てきます。
実際に発生させてみると、
5、2、4、3、6、1、・・・
のような感じです。
これは「サイコロ」のことですよね。
サイコロは一様乱数の発生装置なわけです。
Python で一様乱数を生成してみる
ここではPyhotn のライブラリの1つの NumPy を使って、一様乱数を生成してみます。
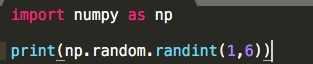
(1行目) numpyをインポートして、npと略して使うようにしています。
(3行目) numpy の中の、random というモジュールを使っています。
この使い方では、1−5までの整数の一様乱数を生成します。
つまり、randint(a, b)として使うと、
(a, b-1)の範囲の整数を乱数として生成することができます。
b の値は生成されないことに注意してください。
np.random.randomint( )1回使うと1個の乱数が生成されます。
複数の一様乱数(乱数列)を生成させてみます。
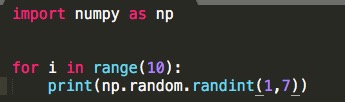
for を使って、繰り返して一様整数乱数を1−6の範囲で生成させています(カッコの中は1−7になっています)
この乱数生成プログラムはサイコロと同じです。
プログラムを実行すると以下のようになります。
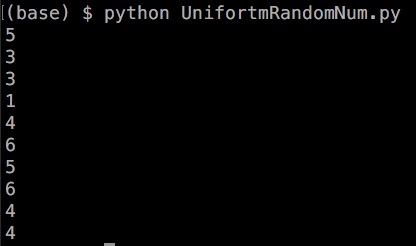
10個生成させてみると、
1、3、4、5、6
が出ています。
- あれ、今回2は出ていないよ?
- 一様(等確率で生成してる)なら2も出るんじゃないの?
と思われるかもしれません。
結論から言うと、
この先は会員限定になります。
会員の方はログインをお願いいたします。
登録がまだの方は、会員登録をお願いします。
>>> 会員登録はこちら
↓こちら無料で読めます















