NumPy は、Python でデータ分析や統計解析を行う時、
生データを分析しやすい形に整理するデータ加工
などを行う時、
行列演算などスムーズに行う時
などに活躍するライブラリです。
ディープラーニングなどの人工知能や機械学習、
時系列分析などでも頻繁に使われます。
NumPy を使いこなすことで、
Python よりもサクッと実装でき、プログラミングが加速させることができます。
データ分析や統計モデリングなどでは、確率分布を扱う機会が多くあります。
NumPyでは、確率分布にしたがった乱数を生成する機能があります。
なんらかの確率分布にしたがったデータを生成することで、
現実を確率論の世界にモデル化して、シミュレーションすることも可能です。
とはいっても、
- 確率分布にしたがった乱数ってなに?
といった方も多いかと思います。
確率分布にしたがった乱数とは?については、
以下の記事でサクッとわかりやすく、解説しています↓
『【Python 数学】確率分布にしたがった乱数とは?について、サクッとわかりやすくまとめました【Python 入門】』
本記事では、
- Python NumPy を使った、確率分布にしたがった乱数の生成方法
について、初学者の方にもわかりやすいように、サクッと、わかりやすく、まとめたいと思います。
【Python NumPy random randn normal】ベクトル・行列の生成・初期化方法(8):正規分布にしたがった乱数の生成・初期化方法(random randn normal)について、サンプルコードとともに、サクッとわかりやすくまとめました【Python 入門】
確率分布といっても、様々なものがあります。
にしたがった乱数を生成する
例えば、以下のものがあります。
- 正規分布
- 二項分布
- ベータ分布
- ガンマ分布
- ポアソン分布
- カイ2乗分布
他にもいろいろありますが、
これらの確率分布は、統計解析やデータ分析などでよく使われるものになります。
ここでは、1番よく使われる基本の確率分布である
- 「正規分布(ベルカーブ)」にしたがった乱数の生成方法
についてご紹介します。
といっても、正規分布について馴染みが薄い方も多いかと思います。
そこで本記事では、
- 正規分布ってなに?
- 正規分布には、どんな例があるの?
- Python NumPy で、正規分布にしたがった乱数の精製方法とは?
といった内容で、初学者の方にも、わかりやすく、サクッと学べるようにまとめます。
正規分布とは?
正規分布は、英語でノーマル・ディストリビューションなんですが、
- ノーマルを日本語にして正規
- ディストリビューションが分布
になります。
ノーマルは、普通の意味もあるように、
- 正規分布は、身の周りによくある分布
です。
図で描くと、以下の感じになります。
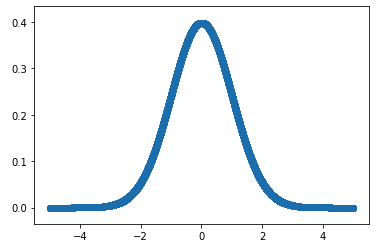
ヨコ軸の値が出る確率がタテ軸に書かれています。
具体的には、例えば、
- 0という値が出る確率は 0,4 くらい
- 2 という値が出る確率は0.1 くらい
といったことがわかります。
このグラフの特徴は、平均を中心(この例では平均0)にして、
左右対称の釣鐘の曲線です。
釣鐘の形なので、ベルカーブとも呼ばれます。
数式で表すと、以下のように描かれます。
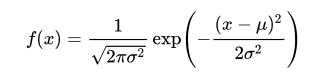
ある値xを考えた時に、
その値が正規分布にしたがって出る確率が
f(x)になります。
図では、ヨコ軸がx、タテ軸 f(x) になります。
f(x)は、xが出る確率を表現しているわけです。
f(x)を正規分布の「確率密度関数」とも言います。
文字がたくさんあるので、わかりにくいかもしれません。
少し解説すると、この式は、2つの式のかけ算になっています。
- 分数×指数関数
の形をしています。
分数部分は
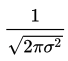
分母にルートがあり、中身は
2×パイ(円周率)×(xの標準偏差の2畳)
となっています。
指数部分は
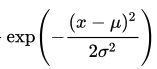
exp( ) は、ネイピア数の指数関数(ex)と同じものです。
ネイピア数はだいたい2.7くらいの値の無理数です。
exの x の部分が複雑な時は、書きにくいので、
exp( )として書く書き方が使われます。
正規分布の式の指数部分では、
( ) の中が分数になっていて、
- 分母には 2×(xの標準偏差の2乗)
- 分子には、xとxの平均値(μ)の差の2乗
があり、マイナスがついています。
この分数を指数関数 exp( ) に与えています。
正規分布の確率密度関数を計算するには、
xとxの平均と標準偏差を求めておき、
上の式に代入して計算すればオッケーです。
この辺は統計学で詳しく学べますので、
興味がある方は統計学の教科書などを参照してみてください。
正規分布の具体例とは?どんな時に使うの?
この先は会員限定になります。
会員の方はログインをお願いいたします。
登録がまだの方は、会員登録をお願いします。
>>> 会員登録はこちら
↓こちら無料で読めます
(Kindle Unlimited にご登録ください)




















