「ニューラルネットワーク」とは、生物の神経回路網からアイデアを得た、人工的なネットワークモデルの1つです。
「ニューラル」は、「ニューロン」という神経細胞からきています。
ニューラルネットという人工的なネットワークの応用例として有名なのは、「画像の分類」などがあります。
画像を分類するためには、画像の特徴を認識する必要があります。
この「画像認識」などと呼ばれるタスクでは、ディープラーニングが非常に良い成績を収めています。
ディープラーニングは人工知能(ai)・機械学習の1つです。
ニューラルネットワークをミルフィーユのように多数積み重ねたネットワーク構造をしています。
ネットワークを複雑化することで、複雑なパターンも認識でき、それにより精度が向上したと考えられています。
なので、ニューラルネットワークとディープラーニングの違いは、ネットワーク構造の層の数が違うことです。
層を多層化した結果、データの複雑な規則性を表現する能力が備わったと言えます。
ニューラルネットワークは、分類問題だけでなく、
「回帰問題」にも使うことができます。
「回帰」とは、データを式で表現することを言います。
「ニューラルネットワーク回帰」を行うことで、データの規則性を表現した数式を得ることができます。
その数式を「ニューラルネットワークモデル」と呼びます。
ニューラルネットワーク回帰の例としては、例えば、
- 気温から売上を予測する
といった一般的なペアのデータのモデル化に使えます。
- ニューラルネットワークの仕組みとは?
- ニューラルネットワークの重み・バイアス・活性化関数ってなに?
- ニューラルネットワーク回帰をPythonなどで実装してみたい
と思われる方も多いかと思います。
そこで本記事では、
- ニューラルネットワークの仕組み
- ニューラルネットワーク回帰のアルゴリズム
- ニューラルネットワーク回帰を Python kerasで実装する方法
などについて、サンプルコードを交えながら、わかりやすくまとめます。
特に、線形回帰と比較しながら説明することで、
- ニューラルネットワーク回帰と線形回帰の違い
を通じて、ニューラルネットワーク回帰のイメージを直感的に理解しやすいかと思います。
加えて、ニューラルネットワークを重ねたディープニューラルネットワークの理解も深まるはずです。
【ニューラルネットワーク Python】ニューラルネットワークとは?種類やモデル、仕組みを学習し、Python で入門・実装したいあなたは、サンプルコードなどもこちらをどうぞ【keras 入門】
ニューラルネットワークの仕組みとは
ニューラルネットワークモデルとは
ニューラルネットワークとは、神経細胞ネットワークからヒントを得た、人工ネットワークです。
その人工ネットワークのことを、
「ニューラルネットワークモデル」と呼びます。
人間の脳内とニューラルネットワークモデルを比較してみます。
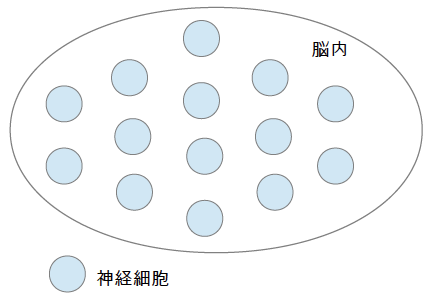
人間の脳内には、神経細胞がたくさん存在しています。
それを模式的に表したのが以下の図になります↓
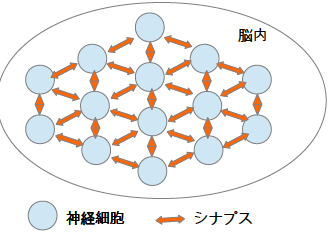
加えて、神経細胞同士は、シナプスという連絡道路でつながっています。
これをオレンジの矢印で書いています。
これをもとに考えられたのがニューラルネットワークモデルになります。
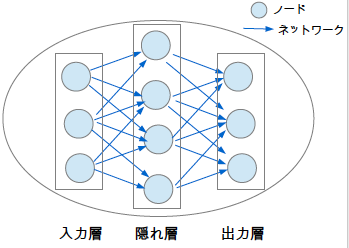
ニューラルネットワークモデルでは、
- 神経細胞のことを「ノード」
- シナプスのことを「ネットワーク」
のように呼ぶことがあります。
ノードは、役割ごとにグループ分けされています。
- 情報の入力を担当する「入力層」
- 入力層から情報を受け取り処理をして出力する「隠れ層」
- 隠れ層から情報を受け取って結果を出力する「出力層」
と呼びます。
(ちなみに、ニューラルネットワークモデルには、他にもいろいろな種類がありますが、ここでは一番基本的なモデルをご紹介しました)
次に、ニューラルネットワークモデルで、
情報が入力から出力まで、どのように伝わるのか説明します。
この先は会員限定になります。
会員の方はログインをお願いいたします。
登録がまだの方は、会員登録をお願いします。
>>> 会員登録はこちら
↓こちら無料で読めます



















